A Mathematical View towards CycleGAN

Recently, CycleGAN is a very popular image translation method, which arouse many people’s interests. Lots of people are busy with reproducing it or designing interesting image applications by replacing the training data. However, few people have thought about its limitations, though the original paper gave some discussions about them.

A failure case of CycleGAN was given by the author himself.

Limitations of CycleGAN

We can actually obtain lots of information from this picture.

• CycleGAN is not able to disentangle the object from the background. Putin and background are both zebraized at the same time, as shown the in the picture.
• CycleGAN is suitable for global image style transfer, but weak at doing object transfiguration. What is object transfiguration? We want to segment a certain part from an image and seamlessly implant it into another images. For example, I want to generate a smiling face of a person by imitating the smile from another smiling face.

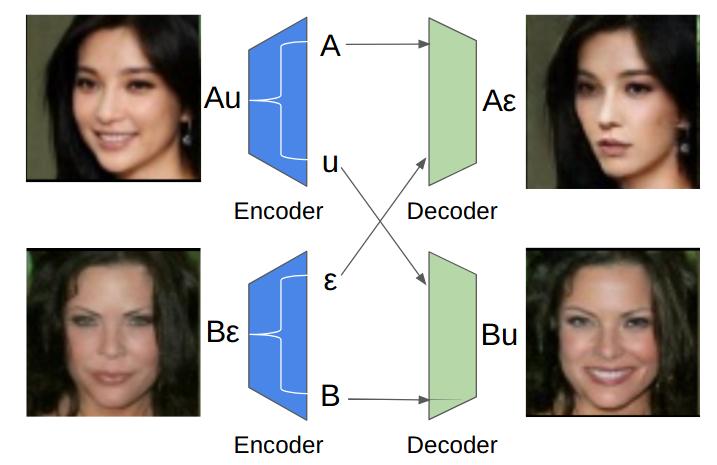
• Lack of diversity in generated images, or single-modal phenomenon. For example, we use CycleGAN to do image translation between two domains. One is facial images without eyeglasses, and the other on is facial images with eyeglasses. CycleGAN can generate novel images with eyeglasses from those images without eyeglasses, but the novel eyeglasses seems always to be a black sunglasses. This phenomenon was observed by Shuchang Zhou, who was very prescient. (see our paper GeneGAN) I believe Jun-Yan Zhu, the author CycleGAN has also noticed this limitation. Otherwise, he would not publish another paper BiCycleGAN to generate multi-modal images in NIPS 2017, right after ICCV 2017 submission deadline, though the idea of BiCycleGAN is somewhat simple and the training process is very similar to IcGAN.
• Weak at learning the shape of object. It is impossible if we want to use CycleGAN to generating a round object from a quadrate object.

The Reason Behind It

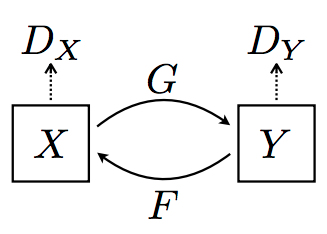
What cause these limitations of CycleGAN? Recall the structure of CycleGAN, there are two image domains $X$ and $Y$. The ultimate goal of CycleGAN is to learn two maps $G$ and $F$, where $G$ maps domain $X$ to domain $Y$, and $F$ maps domain $Y$ to domain $X$.

Recalling a simple result in topology, Invariance of domain theorem states

If $U$ is an open subset of $\mathbb{R}^n$ and $f:U\to \mathbb{R}^n$ is an injective continuous map, then $V = f(U)$ is an open and $f$ is a homeomorphism between $U$ and $V$.

We will leave out the proof since it uses tools of algebraic topology. This theorem tells us an important consequence:

$\mathbb{R}^n$ can not be homeomorphic to $\mathbb{R}^m$ if $m\neq n$. Indeed, no non-empty open subset of $\mathbb{R}^n$ can be homeomorphic to any open subset of $\mathbb{R}^m$ if $m\neq n$.

Back to our discussion of CycleGAN, $G$ and $F$ are generally neural networks with auto-encoder structures, therefore continuous. (The composition of continuous map is continuous.) The cycle consistency guarantees that $G$ and $F$ are inverse to each other. Therefore the domain $X$ and domain $Y$ are homeomorphic. According to the theorem of invariance of domain, the intrinsic dimensions of $X$ and $Y$ should be the same.

This is the fundamental reason for its limitations!!! Because the intrinsic dimensions of $X$ and $Y$ may not be the same.

For example, if we want to do image translation between domain $X$ of facial images with eyeglasses and domain $Y$ of facial images without eyeglasses. Let’s compare the intrinsic dimensions of two domains. The intrinsic dimension of domain $Y$ comes from the variety of facial images. However, the intrinsic dimension of domain $X$ is more than that, because eyeglasses also varies, which increase the intrinsic dimensions.

In conclusion, the limitation of CycleGAN comes from the difference of intrinsic dimensions between source image domain and target image domain. If you are interested, please read our paper GeneGAN for an alternative method.